- Autor admin carl@lifeloveeveryday.com.
- Public 2023-12-16 19:26.
- Ostatnio zmodyfikowany 2025-06-01 06:13.

Przykłady złotego podziału można znaleźć wszędzie w klasycznej architekturze, grafice, naturze, a nawet muzyce. To wyrażenie proporcji, znane również jako Boski współczynnik, zapewnia harmonijną kompozycję poprzez zastosowanie liczby niewymiernej (1,618) w projektach, zarówno naturalnych, jak i stworzonych przez człowieka. Najprawdopodobniej nie zdajesz sobie sprawy z matematyki kryjącej się za pięknem złotego podziału, ponieważ tworzy on obiekty i muzykę, które w naturalny sposób uznasz za przyjemne i nie wymagają żadnych wyjaśnień.
Złoty podział w architekturze
Złoty podział tworzy niemal doskonałe piękno w naturze i sztuce. Kiedy zaczniesz szukać przykładów złotego podziału w życiu codziennym, możesz być zaskoczony wieloma przypadkami jego wykorzystania do stworzenia wielu monumentalnych budynków i budowli. Kiedy w architekturze stosuje się złoty podział, mówi się, że budynek powstaje przy użyciu „architektury sakralnej”. Stosując obliczenia Złotego Podziału do kwadratu, architekci i projektanci są w stanie stworzyć Złoty Prostokąt, który, jak się uważa, ma najbardziej estetyczne proporcje dla ludzkiego oka.
Przykład złotego prostokąta: Partenon

Fidiasz, grecki rzeźbiarz, stosował w swojej twórczości złoty podział, zwłaszcza gdy zaczął pracować z pasmami, które wyrzeźbił tuż nad kolumnami Partenonu. Warto również zauważyć, że na jego cześć nazwano wartość liczbową przypisaną złotemu podziałowi, Phi.
Jeśli zmierzysz zewnętrzne wymiary Partenonu, odkryjesz, że nie tylko tworzy on Złoty Prostokąt, ale także, że pomiędzy kolumnami znajduje się wiele Złotych Prostokątów. Ta sakralna budowla jest pięknym przykładem złotego podziału w architekturze.
Przykład Złotego Trójkąta: Wielka Piramida w Gizie
Złoty podział, złoty prostokąt i złoty trójkąt można znaleźć w doskonałości jednego z Siedmiu Cudów Świata, Wielkiej Piramidy w Gizie. Aby znaleźć złoty podział, musisz podzielić kwadratową podstawę piramidy o połowę i narysować pionową linię przez środek piramidy. Kiedy połączy się to z zakrzywioną stroną piramidy, można łatwo zobaczyć, jak tworzy Złoty Trójkąt ze stosunkiem 1,618, Złotym Podziałem.
Inne przykłady architektury
Można znaleźć wiele przykładów dawnej i współczesnej architektury sakralnej oraz budynków Złotego Podziału.
- Katedra w Chartres - centrum, Francja
- Notre Dame - Paryż, Francja
- Weranda Dziewic - Akropol, Ateny
- Taj Mahal - Agra, Indie
- Budynek Organizacji Narodów Zjednoczonych - Nowy Jork, Nowy Jork
Złoty podział w przykładach sztuki
Można znaleźć wiele przykładów mistrzów malarzy, którzy stosowali złoty podział. Te dzieła doskonałości powstały przy użyciu proporcji Złotych Prostokątów i Złotych Trójkątów. Sztuka stworzona w oparciu o Złoty Prostokąt okazuje się przyjemniejsza dla ludzkiego oka. To jedna z tajemnic otaczających ten idealny prostokąt i Złoty Podział.
Złoty podział w sztuce

Przykłady grafiki złotego podziału obejmują:
- Leonardo Di Vinci - Mona Lisa, Człowiek witruwiański
- Botticelli - Narodziny Wenus
- Michał Anioł - Święta Rodzina, „Dawid”
- Raphael - Ukrzyżowanie
- Rembrandt - Autoportret
- Salvador Dali - Sakrament Ostatniej Wieczerzy, Trwałość pamięci
Używanie złotego podziału w kompozycji artystycznej
W Złotym Prostokącie znajdują się pewne obszary, które są bardziej atrakcyjne wizualnie niż inne obszary. Punkty te odkrywa się przeciągając linię od dolnego rogu prostokąta do przeciwległego rogu i powtarzając ją z drugim dolnym rogiem. Linie te przetną się dokładnie w środku Złotego Prostokąta. Następnie zmierz środek każdej linii, zaczynając od punktu środkowego. Te cztery punkty nazywane są oczami prostokąta (złoty podział). Następnie w obrębie tych punktów zainteresowania (stosunków) rysuje się lub maluje główny punkt obrazu.
Złoty podział w muzyce

Muzyka składa się z wartości liczbowych, a kiedy do stworzenia utworu muzycznego zostanie wykorzystana złota proporcja, staje się żywym przykładem matematyki. Ciąg Fibonacciego jest również powszechny w muzyce:
- W skali jest osiem nut.
- Trzecia i piąta nuta stanowią podstawę akordów.
- Długość, czyli oktawa, dowolnej nuty wynosi 13 nut.
Sekwencja trwa przez cały utwór muzyczny i staje się bardziej złożona, gdy osiąga złoty podział.
Kompozytorzy, którzy stosowali złoty podział
Niektórzy z najbardziej znanych kompozytorów klasycznych, w tym Bach, Beethoven, Chopin i Mozart, używali złotego podziału i sekwencjonowania Fibonacciego w swoich utworach muzycznych. Niektórzy współcześni kompozytorzy, jak Casey Mongoven, eksplorowali w swojej muzyce złoty podział.
Przykłady złotego podziału w przyrodzie

Gdzie w przyrodzie występuje złoty podział? Znajduje się w złotej spirali Fibonacciego, którą można utworzyć za pomocą złotego podziału. Jest to zjawisko powszechnie spotykane w świecie przyrody. Liście rośliny rosną w taki sposób, aby ich jak najwięcej mogło spiralnie wspiąć się na łodygę. Nowy liść tworzy się dopiero po utworzeniu poprzedniego.
- Kaktusy spiralne
- Galaktyki spiralne
- Słoneczniki
Kwiaty z ciągiem Fibonacciego
Niektóre kwiaty mają płatki kwiatów zgodne z ciągiem Fibonacciego:
- Trzy płatki:Irys, lilia, orchidee, trillium
- Pięć płatków: Jaskry, pelargonie, hibiskus, powój, nasturcja
- Osiem płatków: Ostróżki
- 13 płatków: Niektóre odmiany stokrotek, starców, nagietków
Spirala Fibonacciego w szyszkach

W zależności od gatunku drzewa, można także zobaczyć działanie złotego podziału w ciągu liczb Fibonacciego w szyszkach. Po jednej stronie szyszki można znaleźć osiem spiral, a po drugiej 13 spiral. Inny wzór szyszki ma pięć spiral po jednej stronie i osiem po drugiej.
Złoty podział u ludzi
Ten stosunek jest również ważny nie tylko dla tego, jak ludzie postrzegają siebie nawzajem, ale także dla tego, jak działają ich ciała i ich DNA.
DNA ujawnia złoty podział
Jeden z najbardziej niesamowitych przykładów złotego podziału znajduje się w strukturze ludzkiego DNA. Można to zobaczyć na pojedynczym przekroju DNA, który ukazuje, że podwójna helisa DNA tworzy kształt dziesięciokąta. Jest to połączenie dwóch pięciokątów, obróconych względem siebie o 36 stopni, tworzących podwójną helisę DNA. Sama spirala podwójnej helisy tworzy pięciokąt. Nawet pojedyncza cząsteczka DNA ujawnia podstawę złotego podziału lub boskiej proporcji.
Matematyka złotego podziału
Znalezienie złotego podziału w prawdziwym życiu jest proste, ponieważ pojawia się ono wokół ciebie. Jest to matematyczny truizm używany do zdefiniowania tak zwanej liczby doskonałej występującej w przyrodzie, która była powielana i naśladowana przez ludzi od wieków. Uproszczone piękno tej liczby maskuje jej złożoność wykonania. Aby zrozumieć teorię złotego podziału, musisz najpierw zapoznać się z sekwencją Fibonacciego.
Ciąg Fibonacciego i złoty podział
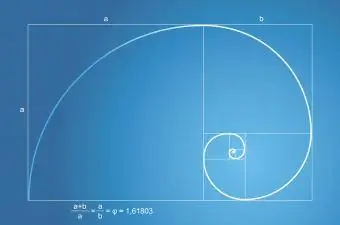
Ciąg lub seria Fibonacciego ma związek ze złotym podziałem. Seria Fibonacciego pokazuje liczbę liści rośliny i liczbę płatków kwiatu. Spirala Fibonacciego występująca w przyrodzie jest zawsze częścią złotego prostokąta ze złotym podziałem.
Matematyka ciągu Fibonacciego jest prosta:
- Sekwencja zaczyna się od 0 i 1.
- Po prostu dodaj do siebie dwie ostatnie liczby, aby otrzymać następną liczbę w serii.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8 i tak dalej.
- Ten przykład ciągu Fibonacciego wygląda następująco: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 i tak dalej.
Związek Fibonacciego ze złotym podziałem staje się widoczny, gdy jest on dodawany coraz dalej i dalej. Im więcej dodasz serii, tym bliżej będziesz złotego podziału.
Tworzenie złotego prostokąta i trójkąta
Aby utworzyć złoty prostokąt z ciągu Fibonacciego, zacznij od kwadratu. Zaczniesz budować prostokąt, dodając kolejny kwadrat do pierwotnego kwadratu. Pamiętaj o zastosowaniu wzoru: 0+1=1 to pierwszy kwadrat, 1+1=2 - dodasz kolejny kwadrat.1+2=3 dodasz trzy kwadraty, a następnie 2+3=5 dodasz pięć kwadratów. Będziesz nadal dodawać kwadraty, aż w końcu utworzysz Złoty Prostokąt.
Złoty Trójkąt można utworzyć dzieląc Złoty Prostokąt na pół od jednego rogu do przeciwległego rogu. Tworzy to trójkąt, którego trzy boki lub kąty mają proporcję 2:2:1, co oznacza, że dwa długie boki mają równą długość, a krótki kąt ma dokładnie połowę długości dwóch dłuższych.
Złoty podział w prawdziwym świecie
Złoty Podział jest często nazywany Boskim Podziałem ze względu na jego znaczenie w przyrodzie i ludzkich ciałach. Odkrycie, że złoty podział jest obecny w tak wielu żywych istotach, wzbudziło szacunek dla tej magicznej proporcji i nadal stanowi inspirację dla współczesnych artystów i twórców.